OPTIQUE DE FOURIER
PRINCIPE
SPECTRE DU SIGNAL
La représentation de l'amplitude des harmoniques en fonction de la fréquence f (ou de la pulsation ω = 2π f) constitue le spectre du signal :

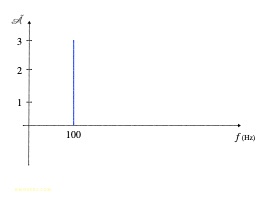
Une onde pure monochromatique est parfaitement sinusoïdale de fréquence constante : son spectre ne présente donc qu'une unique harmonique, la fondamentale, et sa représentation spectrale est du type :

En musique, le signal sonore délivré par un diapason est un son pur : sa hauteur est la fréquence f de l'onde périodique émise, c'est à dire la fréquence du fondamental dans la décomposition de Fourier de cette onde.
Le 'la' d'un diapason correspond à la fréquence
f = 440 Hz. Le double de cette fréquence correspond au la de l'octave supérieure (880 Hz) et la moitié de cette fréquence au la de l'octave inférieure (220 Hz).
Mais le timbre d'une note de même hauteur peut différer selon l'instrument qui le joue : il dépend de sa composition spectrale (nombre, magnitude et durée des harmoniques [ largeur de la bande spectrale ]) et de son évolution au cours du temps.
Une onde courbe complexe peut être décomposée en composantes spectrales d'ondes planes (fig 4). Chaque composante spectrale correspond à une onde plane, à une fréquence spatiale donnée, qui va se propager comme une onde plane.
La résolution d'un système optique va être définie par la taille de la pupille d'entrée : plus elle est large, plus le signal analysé va être important.
Une analyse de Fourier correspond à une décomposition du spectre d'un signal en fonction de la fréquence de ses sinusoïdes. Les séries de Fourier s'appliquent aux fonctions périodiques. La transformée de Fourier est l'outil mathématique qui permet cette décomposition pour n'importe quelle fonction.
Tout signal dépendant du temps peut être décrit comme une somme de pures sinusoïdes : il est possible de décomposer un signal u(t) de fréquence f associé à la propagation d'une onde périodique non sinusoïdale, en une somme infinie de signaux sinusoïdaux. Tel est le principe de la décomposition de Fourier du signal.
Représentons en jaune un signal périodique u(t) quelconque :
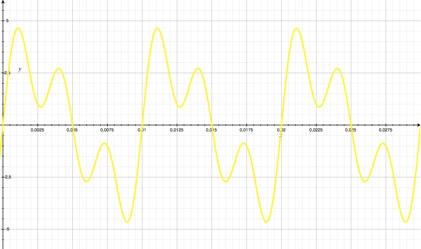
Il est de période T = 10 ms = 10-2 s donc de fréquence f = 100 Hz.
Il peut se décomposer comme la superposition de signaux sinusoïdaux de la forme :
N
Σ ak cos (n ωt) + bn sin (n ωt) = Σ an cos (2π n f t) + bn sin (2π n f t)
n=0
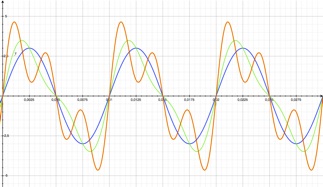
Dans l'exemple simple choisi ici, le signal jaune peut se décomposer comme la somme suivante : u(t) = 3 sin (2π.100.t) + sin (2π.200.t) + 2 sin (2π.300.t)
➭ Le signal sinusoïdal 3 x sin (2π.100.t)
-
à la fréquence f
-
est nommé "fondamentale"
-
ou "première harmonique".
-
Il est représenté en bleu.
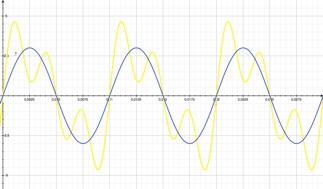
➭ Le signal sinusoïdal 1 x sin (2π.200.t)
-
à la fréquence 2 f
-
est nommé "deuxième harmonique".
-
La somme des deux premières harmoniques est représentée en vert. On constate que l'aspect global se rapproche de l'onde u(t) jaune.
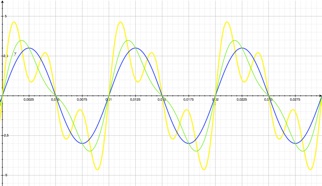
➭ Le signal sinusoïdal 2 x sin (2π.300.t)
-
à la fréquence 3 f
-
est nommé "troisième harmonique".
-
La somme des 3 premières harmoniques est représentée en rouge. Cette courbe rouge est confondue avec le tracé de l'onde u(t) jaune :
-
l'onde u(t) comporte donc "seulement" 3 harmoniques.
-
Les harmoniques sont des signaux sinusoïdaux de fréquence fn = n f.
-
Le nombre n est un entier positif appelé "rang" de l'harmonique.
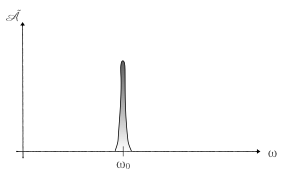
La largeur de la bande spectrale ω0 pour une onde "monochromatique" A (t) = A0 cos (ω0t) en analyse de Fourier n'est en réalité jamais nulle, car il existe toujours une certaine dispersion autour d'une pulsation centrale de référence. C'est donc une onde "quasi-monochromatique".

La plupart des mesures de signaux dépendent du temps.
Mais cette analyse en fonction du temps est rarement intéressante. Grâce à Fourier, il est également possible de mesurer les répétitions en fonction des périodes, c'est à dire des fréquences. Comme si "l'oreille absolue" -qui permet de reconnaître la fréquence exacte d'une note- était donnée à tout signal dépendant du temps.
Les applications des transformées de Fourier ne concernent pas que les fréquences sonores mais s'étendent à toutes les répétitions, dont le traitement d'image numérique que nous utilisons quotidiennement (smartphones, internet, photos et caméras numériques...).
