MGUEDJ.COM

MIKAEL GUEDJ

LEXIQUE ET FORMULES D’OPTIQUE  ONDULATOIRE

⦁ ONDE MONOCHROMATIQUE («μoνo» «𝛘𝜌oμoσ», littéralement "une seule couleur") :

  désigne toute onde dont le vecteur d'onde k est de module constant,

  et ayant une seule fréquence ν (onde harmonique parfaitement sinusoïdale),

  donc une seule pulsation ω bien déterminée et infinie dans le temps !


  Elle s'écrit (en notation réelle) :   A (t) = A0 cos (ωt)     ou  A (r, t) = Am cos (ωt + Φm)

         ou en notation complexe :    A (t) = A0 e i ωt         ou  A (r, t) = Ak e i (ωt - k.r + Φk)

🅐 LEXIQUE

⦁ COHÉRENCE TEMPORELLE : c = 1/Δν

  1. inversement proportionnelle à la largeur de bande spectrale Δν de la source.

  2. Une onde théorique purement monochromatique (une seule fréquence, bande spectrale fréquentielle hyperfine) aurait un temps de cohérence infini ( c = 1/Δν ).

  3. La longueur de cohérence temporelle s’écrit Lc = c  . v  (vitesse de propagation de l’onde).

  4. Si les chemins optiques ont une différence supérieure à cette valeur Lc, on dit que la différence de marche est supérieure au train d’onde (Lc), il n’y aura pas d’interférences.

⦁ COHÉRENCE SPATIALE : ls = λD /ΔS

  1. capacité de chacun des points du front d’onde d’interférer avec un autre point.

  2. La largeur de cohérence  de la source ls dépend de caractéristiques intrinsèques de la source (longueur d’onde λ et ΔS (largeur de la distribution spatiale d’intensité)) et de paramètres expérimentaux (la distance à l’écran (D)).

⦁ TRAIN D’ONDES (ou paquet d'ondes) :

  1. onde dont l'étendue spatiale (Lc) et temporelle (c) est finie. Elle est due au fait que les atomes n'émettent de la lumière cohérente que pendant un temps fini.

⦁ DÉPHASAGE :

  différence de phase entre 2 ondes      ΔΦ = Φk - Φj 

⦁ DIFFÉRENCE DE MARCHE : 

  différence de longueur des chemins optiques parcourus    δ = r1 - r2 

⦁ INTENSITÉ  LUMINEUSE :

   c'est la quantité d'énergie transportée par l'onde lumineuse, aussi appelée éclairement.

   Elle se définit comme la valeur moyenne du produit de A par son conjugué A* ,

   sur un temps long comparé à la période T.

   En notation complexe, elle s'écrit :

    I = < A A*> = A0 e i ωt . A0 e - i ωt  = A0 2

    

     En notation réelle,  A2 = A02 cos2 (ωt)    

     et sa moyenne <A2 > = A02 <cos2 (ωt)> = 1/2 A02

       donc  I = 2 <A 2 > = A0 2  en écriture réelle


    De plus, la somme de 2 sources monochromatiques S1 et S2

     de même amplitude A0 et de phases respectives Φ1 et Φ2 peut s'écrire :

     A total (t) =  A0  [ cos (ωt + Φ1) + cos (ωt + Φ2) ]

     A total (t) = 2 A0 [cos ((ω t + (Φ1 + Φ2) /2 )   cos ((Φ1 - Φ2) /2)]    

      A 2tot  = 4 A0 2  [ cos 2 (ω t + (Φ1 + Φ2) /2 )   cos 2 (Φ1 - Φ2) / 2) ]

                 avec à chaque changement de phase A2max = 4 A0 2  cos 2 (Φ1 - Φ2) / 2)

                 car le premier terme cos 2 (ω t + (Φ1 + Φ2) /2 ) varie entre 0 et 1 (1 = maximum).

       La moyenne de chaque valeur A maximum est donc 1/2 de 4 A0 2  cos 2 (Φ1 - Φ2) / 2)

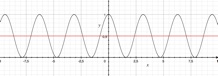
       et la moyenne d'une fonction cos2(x) quelconque est égale à 1/2 (voir le graphe ci-dessus)

   ⇒   Itot = 2 <Atot 2 > = 2 <(1/2) (1/2) 4 A0 2 > = 2 A0 2  = 2 I0

La moyenne de la fonction cos2(x) est de 1/2
 

⦁ ONDE PROGRESSIVE :

  onde qui se propage dans l'espace au cours du temps

⦁ ONDES ISOCHRONES :

  ondes qui ont la même pulsation ω.

⦁ ONDES SYNCHRONES :

  ondes isochrones présentant un déphasage constant au cours du temps,

  donc une même longueur d'onde λ.

⦁ ONDE :

  1. propagation d'une perturbation transportant de l'énergie sans transport de matière, survenant dans un milieu matériel (pour les ondes mécaniques) ou non matériel (pour les ondes électromagnétiques, pouvant se propager dans le vide).

⦁ APPROXIMATION PARAXIALE : 

  1. lorsque la distance entre l'objet et le système optique est grande devant à la fois la taille de l'objet et celle du système optique, les spectres angulaires observés ne sont pas extrêmes.

  2. A (r, t) = Ak e i (ωt - k.r + Φk) s'écrit  A (z, t) = Az e i (ωt - k.z + Φz)

⦁ OPACITÉ :