INTERFERENCES
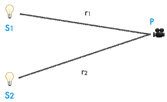
A total (t) = (a / r1) e i(ω1t - k1 r1) + (a / r2) e i(ω2t - k2 r2)
Approximation : r1 ≃ r2, ie ∣ r1-r2 ∣ << r1 , d’où :
A total (t) ≃ (a / r1) [ e i(ω1t - k1 r1) + e i(ω2t - k2 r2) ]
dont la partie réelle s’écrit :
A total (t) ≃ (a / r1) [ cos (ω1t - k1 r1) + cos (ω2t - k2 r2) ]
ou encore, avec A0 = amplitude liée à une seule source et Φ = phase = k.r :
A total (t) ≃ A0 [ cos (ω1t + Φ1) + cos (ω2t + Φ2) ]
Or cos a + cos b = 2 cos (a+b /2) cos (a-b /2), d’où :
A tot (t) ≃ 2 A0 [cos ((ω1 + ω2) /2 . t - (Φ1 + Φ2) /2 ) cos ((ω1 - ω2) /2 . t - (Φ1 - Φ2) /2)]
Si ω1 et ω2 sont du même ordre de grandeur (10 15 en optique),
le premier terme cos (en bleu) va osciller très rapidement (ω1 + ω2),
alors que le second terme cos (vert) oscillera très lentement (ω1 - ω2).
Le produit des 2 termes est un «battement», représenté sur le schéma ci-dessous :
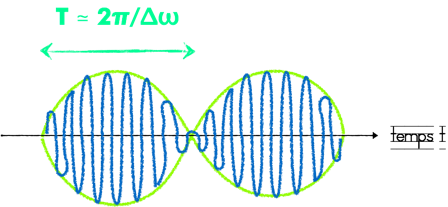
Ces battements sont audibles aux fréquences acoustiques usuelles (accordage d’un instrument à cordes), mais ne sont pas observables en optique, car pour 2 sources lumineuses distinctes, Δω n’est jamais assez petit pour qu’on observe les battements.
PRINCIPE
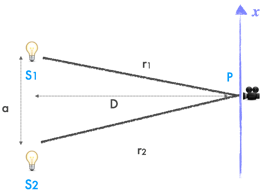
Dans cette configuration où D >> a et D >> x, et r1 ≃ r2, on a r2 - r1 ≃ ax / D ;
L’intensité totale peut donc s’écrire :
I tot (t) ≃ 4 I0 cos2 ( π a x / λD )
On obtient un ensemble de franges d’interférences :
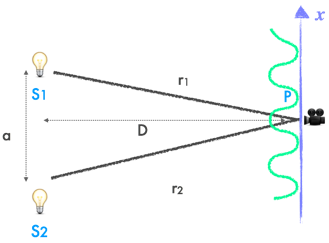

dont l’interfrange (distance entre 2 franges) aux maximums d’intensité (pour que cos = 1) est :
interfrange = λD / a

A1 (t) ∝ e i(ω1t)
A2 (t) ∝ e i(ω2t)
A total (t)
Pour des sources identiques de même pulsation
ω1 = ω2 = ω
et k1 = k2 = k
A tot (t) ≃ 2 A0 [ cos (ω t + (Φ1 + Φ2) /2 ) cos (Φ1 - Φ2) / 2) ]
avec :
A max ≃ 2A0 cos (k (r2 - r1) / 2) puisque le premier terme cos (ωt+...) varie entre 0 et 1
C’est le principe des casques audio «anti-bruit» qui ajoutent une interférence destructive de phase opposée au bruit ambiant recueilli, pour que la somme des interférences soit nulle.
L’intensité totale I s’écrit donc :
I tot (t) = A 2tot = 4 A0 2 [ cos 2 (ω t + (Φ1 + Φ2) /2 ) cos 2 (Φ1 - Φ2) / 2) ]
I tot ≃ 4 I0 cos2 (k (r2 - r1) / 2) ≃ 4 I0 cos2 (k δ / 2) donc I tot (t) ∈ [ 0, 4 I0 ]
En clair, la somme de 2 ondes lumineuses peut de façon surprenante produire de l'obscurité ! L'intensité totale est alors égale à 0 au niveau du détecteur (au niveau des franges d’obscurité).
A l'inverse, elle peut aussi être égale à 4 fois l’intensité lumineuse de chaque source au niveau des franges hyperlumineuses.
C’est le principe des interférences démontré par l’expérience des fentes de Young (voir plus bas).
Calcul avec les notations complexes
L’amplitude totale s’écrit :
A tot (t) ≃ A0 [ e i (ω t - k r1 ) + e i (ω t - k r2 ) ]
et le complexe conjugué (i remplacé par -i) :
A *tot (t) ≃ A0 [ e - i (ω t - k r1 ) + e - i (ω t - k r2 ) ]
L’intensité est la valeur moyenne de A x A* :
I = <A tot A *tot > = A0 2 [ 1 + 1 + e i k (r2 - r1 ) + e - i ik (r2 - r1 ) ]
= 2A0 2 [ 1 + cos (k (r2 - r1)) ]
Figures d’interférence
L’intensité totale peut donc s’écrire comme :
I tot (t) ≃ 4 I0 cos2 (k (r2 - r1) / 2)
On note que lorsque r1 = r2 (cos 0 = 1), la médiatrice de S1S2 est un 1er plan simple d’intensité maximale.
Les autres surfaces d’intensité maximale (telles que cos = 1) doivent vérifier :
δ = r2 - r1 = 2π / k = λ
La figure représentant ces lieux d’égale intensité dans l’espace au voisinage de 2 sources S1 et S2 est un ensemble d’hyperboloïdes de révolution :

ou en représentation 3D :

Si l’on place un écran au dessus, dans l’alignement des 2 sources, on observe des interférences circulaires. On les appelle des «anneaux d’interférences» :
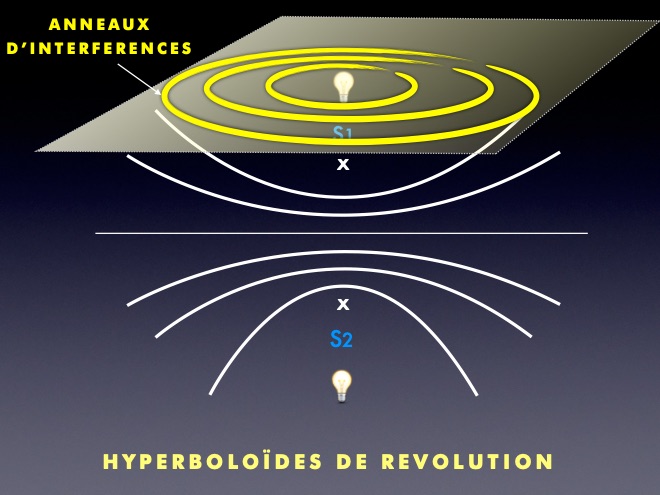
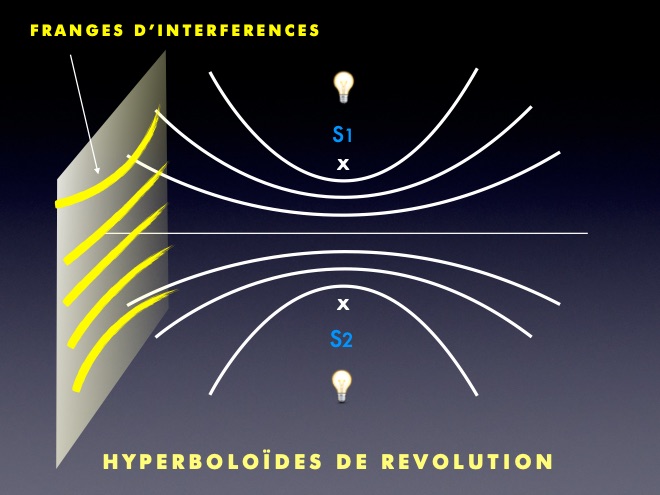
Si l’on place l’écran sur le côté, parallèlement à l’axe rejoignant les 2 sources, on observe des interférences linéaires. On les appelle des «franges d’interférences» :
A1 (t) ∝ e i(ω1t)
A2 (t) ∝ e i(ω2t)
Atotal (t)
Considérons 2 sources lumineuses S1 et S2, d’amplitude A, recueillies par un détecteur au point P :
La superposition de 2 ondes monochromatiques recueillies au niveau d’un détecteur s’écrit sous la forme d’une équation d’onde linéaire :
MIROIRS DE FRESNEL
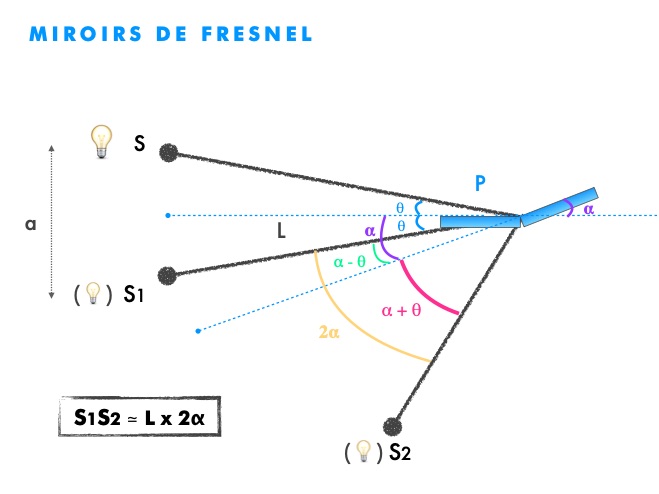
Les miroirs de Fresnel sont un dispositif interférentiel composé de 2 miroirs formant un angle α < 1°, comme représentés sur les schémas suivants :
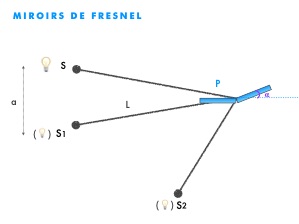
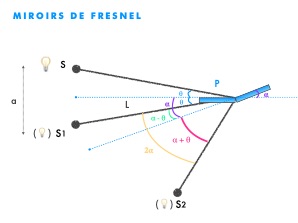
S1 S2 = 2 L sinα ≃ L . 2α pour des angles α très petits
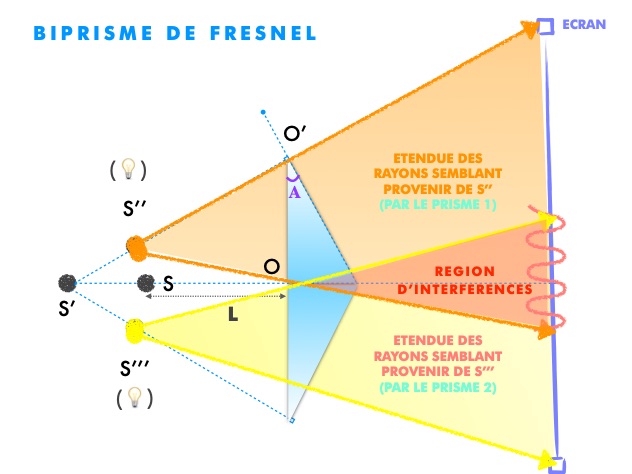
BIPRISME DE FRESNEL
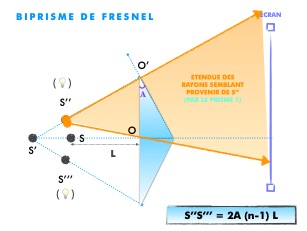
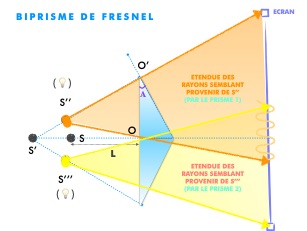
Le biprisme de Fresnel est un dispositif interférentiel composé de 2 prismes d’angle défini A, à une distance L de la source S, comme l’explique la succession des schémas suivants :
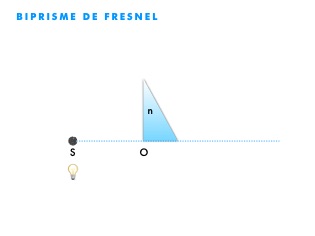
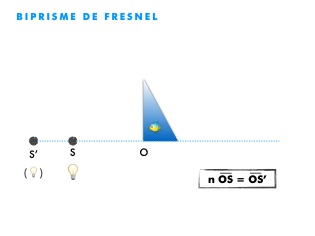
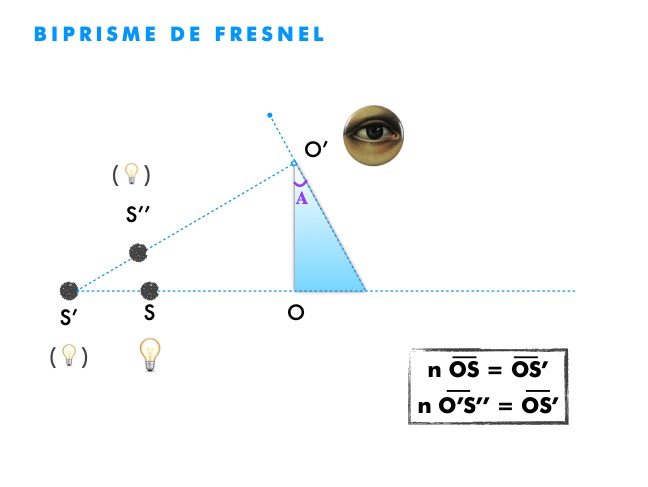
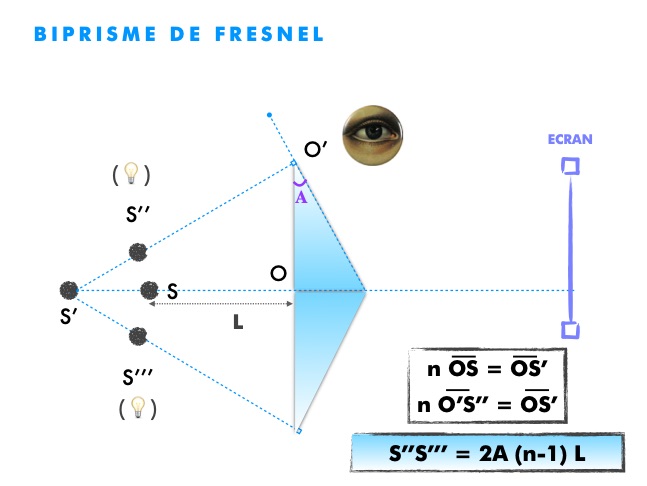
S’’S’’’ = 2 A (n-1) L
DISPOSITIFS INTERFERENTIELS
TROUS DE YOUNG
L’expérience des trous de Young (ou fentes de Young) fait intervenir le phénomène de diffraction au niveau de chaque trou (ou fente) pour créer des interférences. Elle sera détaillée au chapitre «Diffraction».
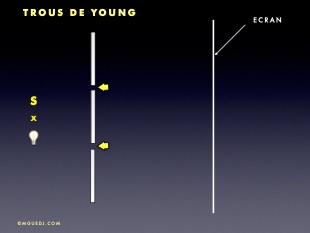


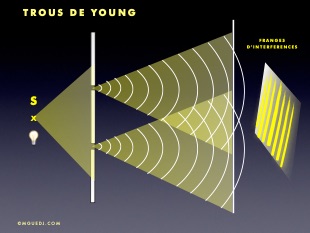

La superposition de 2 ondes en un point M génère une perturbation équivalente à la somme des deux perturbations incidentes. Après le point M, les 2 perturbations continuent leur ondulation sans être modifiées.
Il y a interférence en tout point M d'un milieu où 2 ondes de même fréquence se superposent :
A total (M, t) = A1 (M,t) + A2 (M,t).
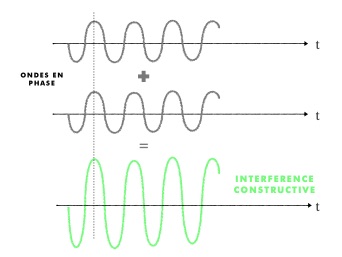
Si les 2 ondes de même fréquence ont un décalage temporel nul ou multiple de la période T, elles arrivent en phase au point M : l'amplitude de la résultante est alors maximale, il y a interférence constructive.
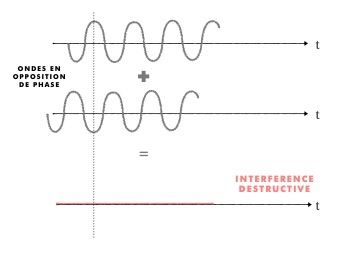
Si les 2 ondes de même fréquence ont un décalage temporel multiple impair d'une demi-période ie (2n+1) T/2 tel que le maximum de l'une coïncide avec le minimum de l'autre, elles sont en opposition de phase au point M : l'amplitude de la résultante est alors minimale, il y a interférence destructive.
