COHÉRENCE
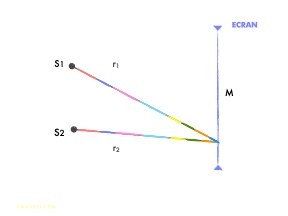
Lorsque la différence de marche S2M - S1M est trop grande, elle superpose au point M
2 trains d'onde différents (couleur bleue + couleur orange), rendant toute interférence impossible entre les 2 ondes.
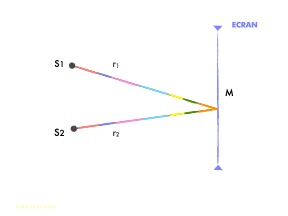
Un point peu décalé du centre de l'écran est toujours le siège d'interférences car 2 trains d'onde de même phase (couleur orange) s'y rencontrent encore.
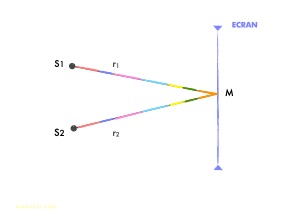
Le point M au centre de l'écran est le siège d'interférences car 2 trains d'onde de même phase (couleur orange) y parviennent en même temps
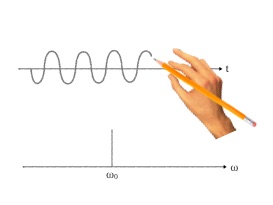
TRAINS D'ONDE

TEMPS ET LONGUEUR DE COHERENCE
-
• Loin du centre de l'écran, le terme Φ1 - Φ2 n'est plus nul et oscille en permanence dans le temps, donc la moyenne du terme
< cos [ k (r1 - r2) + (Φ1 - Φ2) ] > devient nulle (étant le cos d'une variable aléatoire).
On a donc I = <A A * > = 2 I0
⇒ Il n'y a plus d'interférences.
On parle de brouillage en périphérie, au delà des zones centrales interférentielles.
La cohérence temporelle est perdue.
L’amplitude totale s’écrit toujours :
A tot (t) ≃ A0 [ e i (ω t - k r1 - Φ1) + e i (ω t - k r2 - Φ2) ]
et le complexe conjugué (i remplacé par -i) :
A *tot (t) ≃ A0 [e - i (ω t - k r1 - Φ1) + e - i (ω t - k r2 - Φ2) ]
L’intensité est la valeur moyenne de A x A* :
I = <A A * >
= 2 I0 + 2 I0 < cos [ k (r1 - r2) + (Φ1 - Φ2) ] >
= 2 I0 (1 + < cos [ k (r1 - r2) + (Φ1 - Φ2) ] >)
2. COHÉRENCE SPATIALE
Une source purement théorique monochromatique continue dans le temps (émise depuis la nuit des temps et jusqu'à la fin des temps) devrait donner un train d'ondes infini et seul pic de fréquence (ou de pulsation) dans le domaine de Fourier.
Dans un modèle un peu plus réaliste, la superposition de plusieurs sources monochromatiques avec des phases relatives aléatoires légèrement différentes donne un ensemble de trains d’ondes qui n’ont pas de relation de phase entre eux : ce sont des sources "quasi-monochromatiques". Chaque train d'onde de phase différente est représenté par une couleur différente sur le schéma
L’expérience des trous de Young (ou fentes de Young) fait intervenir le phénomène de diffraction au niveau de chaque trou (ou fente) pour créer des interférences. Elle sera détaillée au chapitre «Diffraction».
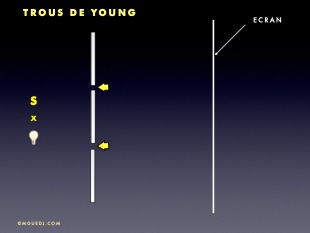


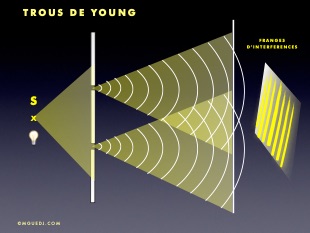

La largeur du train d'onde est appelée "temps de cohérence" et notée ������c :
������c ≃ 1/Δν
������c est inversement proportionnel à la largeur spectrale de la source (Δν) .
Il est de l'ordre de 10-10 s (c'est à dire que l'onde change de phase aléatoirement toutes les 10-10 s).
La "longueur de cohérence" lc s'écrit :
lc = c.𝝉c
Elle est de l'ordre du cm (3. 10-2 m) (c'est à dire que l'onde change de phase aléatoirement toutes les 3 cm).
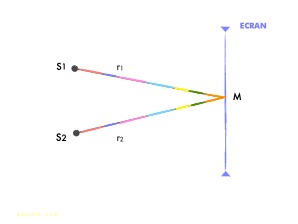
A1 = A0 e -i ωt e i kr1 + iΦ1
A2 = A0 e -i ωt e i kr2 + iΦ2


δ
= différence
de marche
ΔΦ
= différence
de phase
-
• Au centre de l'écran, lorsque les ondes sont en phase, Φ1 = Φ2 , la valeur Φ1 - Φ2 = 0, d'où :
Itot = 2 I0 (1 + < cos [ k (r1 - r2) + 0 ] >)
⇒ On y retrouve des interférences
(voir le chapitre "Interférences").
Les ondes sont dites "temporellement cohérentes".
➭ Il ne suffit pas d'avoir 2 sources de même fréquence pour observer des interférences, il faut également que les sources aient la même phase (les mêmes trains d'ondes) !
Or, il est impossible en pratique d'émettre des mêmes trains d'onde (en phase) avec 2 sources différentes, même monochromatiques pures de fréquence identique (de type lasers).
Il convient donc de prendre 2 images de la même source pour obtenir des interférences, comme sur les dispositifs interférentiels expliqués au chapitre précédent.
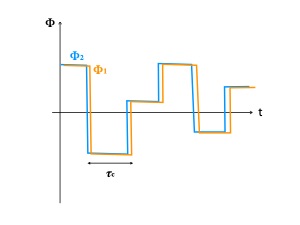
Au centre de l'écran,
la différence de phase Φ1 - Φ2
est quasiment nulle en tout point
(les 2 courbes sont superposées) :
Itot = 2 I0 (1 + < cos [k (r1 - r2)] >)
C'est une situation d'interférences.
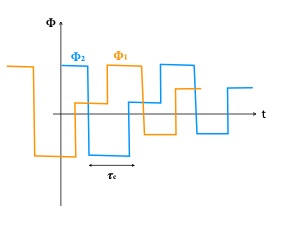
En s'éloignant du centre de l'écran,
les trains d'ondes sont en décalage, la différence de phase Φ1 - Φ2 n'est plus nulle et la moyenne du <cos> de ce terme aléatoire est nulle :
Itot = 2 I0
Il n'y a plus d'interférences.
1. COHÉRENCE TEMPORELLE
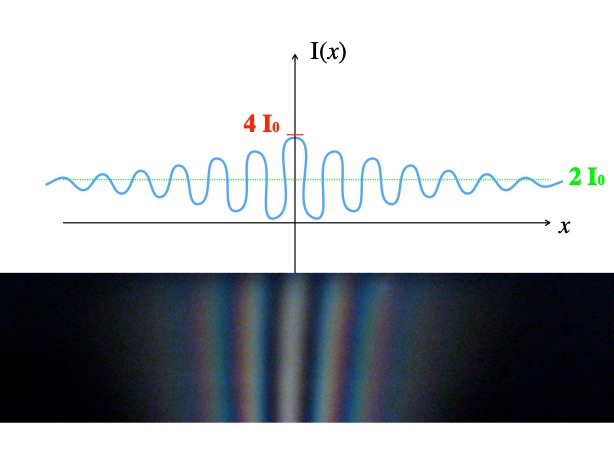
Le centre de l'écran est le siège d'interférences bien visibles (alternance de bandes colorées hyperclaires et de bandes sombres) liées au fait que les trains d'onde ont la même phase : les ondes sont dites "temporellement cohérentes". Le maximum d'intensité, au centre, correspond à la valeur 4 I0.
Trop loin du centre, les interférences ne sont plus visibles : la cohérence temporelle est perdue, avec une clarté moyenne uniforme d'intensité 2 I0 en périphérie. C'est le "brouillage".
BROUILLAGE
BROUILLAGE


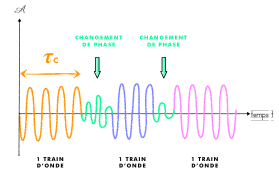
Deux sources sont cohérentes si elles émettent des ondes sinusoïdales de même fréquence et si le retard de l'une par rapport à l'autre ne varie pas au cours du temps : elles gardent alors un déphasage constant.
