Une onde se propage autour d'une source dans une, deux ou trois dimensions : elle dépend alors d’une position dans l’espace (M (x,y,z)) et du temps (t). Elle est représentée comme un signal (ou une vibration) noté s (M,t) ou encore s (x,y,z,t).

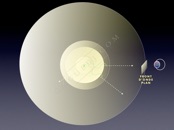
Une onde plane ne dépend que d’une seule coordonnée cartésienne de l’espace, et s’écrit par exemple s (x,t) si elle vibre selon x et indépendamment de y et de z. Même si une onde parfaitement plane est purement théorique, on assimile souvent en optique ondulatoire une surface d’onde sphérique de grand rayon à une surface plane tangente à ce rayon, comme le représente le schéma voisin.

Pour une onde plane, tous les points d'un même plan d'onde sont en phase.

Une onde plane progressive répond à une équation de propagation :

x

x

x’

x

x’

Un mouvement périodique est un mouvement qui se répète à intervalles de temps égaux.

La période d'un phénomène périodique est la durée au bout de laquelle le phénomène se répète identique à lui-même. Elle se note T et s'exprime en secondes (s).

La fréquence d'un phénomène périodique représente le nombre de phénomènes survenus par seconde. Elle se note f ou ν et s'exprime en hertz (Hz = s-1).

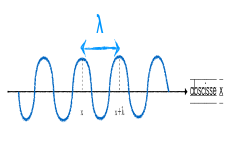
La longueur d'onde est la distance parcourue par l'onde un une période temporelle T.

Elle se note λ et s'exprime en mètres (m).

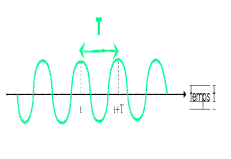
Une onde plane progressive périodique présente une double périodicité :

  Périodicité temporelle avec une période T minimale telle que :

  donc  2π f T = 2π, d’où la période temporelle (T) et la pulsation (ω):

  Périodicité spatiale avec une longueur d’onde λ minimale :

  donc  2π λ f /v = 2π,   d’où  la longueur d’onde (λ) :

  λ correspond donc à la distance (en mètres) parcourue par l’onde

entre 2 points à la célérité c pendant une période temporelle T.

On définit le vecteur position r = OM et le vecteur d’onde k (direction de propagation de l’onde),

de norme   k = ω / c  =  2π / cT  =  2π / λ   

Le signal peut donc s’écrire sous une forme vectorielle indépendante du système de coordonnées :

  ou en notation complexe :

Si l’onde n’est pas harmonique (ou monochromatique), elle pourra être considérée comme la superposition d’ondes harmoniques monochromatiques grâce aux transformées de Fourier.

  ex:   n air ≃ n vide = 1     ;    n eau = 1,33    ;   n verre = 1,50

Dans le vide (n = 1), la longueur d’onde associée à la période T est    λ0  =   c / f   =   c T

Dans un milieu d’indice n, la longueur d’onde associée à la période T est    λ  =  v / f  =  v T  =  c / nf  =  λ0 / n

Plus l’indice de réfraction est élevé, plus le retard de phase induit est important :

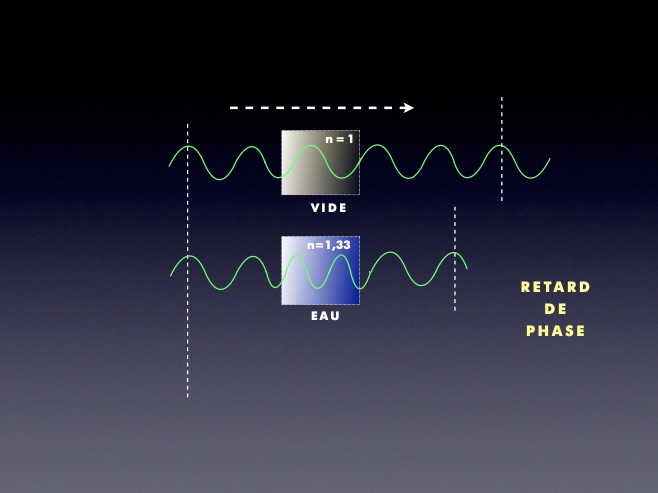
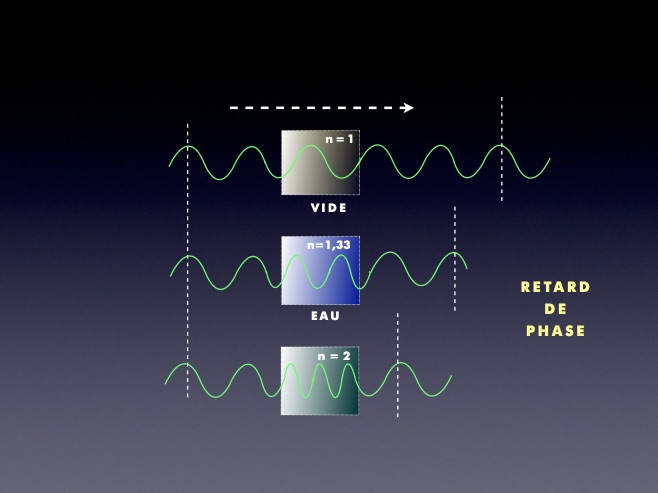
La longueur d’onde λ varie selon les milieux traversés ( λeau < λair ),

de même que sa célérité c et son nombre d'onde k,

mais l’onde garde la même amplitude et la même fréquence f d’un milieu à l’autre.

Le vecteur d’onde k est colinéaire au vecteur unitaire u, normal à la surface d’onde :

Dans un milieu isotrope, les rayons lumineux sont en tout point perpendiculaires aux surfaces d’onde.

Le déphasage entre 2 ondes peut être relié à la différence de chemin optique parcouru selon les 2 voies d’un dispositif interférentiel :

A ce déphasage géométrique, il faut ajouter un déphasage supplémentaire lié à la rencontre d’une interface optique si l’onde est réfléchie d’un milieu moins réfringent sur un milieu plus réfringent (air ➡ eau) :

Une onde plane progressive est dite harmonique (ou «monochromatique» ) si s (x,t) est une fonction sinusoïdale du temps et de l’espace : une onde monochromatique a donc une fréquence et une pulsation bien déterminées.

Dans le sens des x croissants, le signal s’écrit :